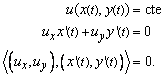Funciones de Variable Compleja (FVC)

Campos Eléctricos y Funciones Analíticas

Teoría del Potencial: Ecuación de Laplace

En la física del siglo XIX, se creía que las fuerzas fundamentales de la naturaleza estaban regidas por “potenciales” que satisfacían la ecuación de Laplace:

Se conocía en ese entonces a la Teoría del Potencial como el estudio de las funciones que podían servir como potenciales. Hoy en día se sabe que la naturaleza es aún más complicada, pero sin embargo se sigue utilizando dicha ecuación para la resolución de problemas de campos gravitaciones, campos electrostáticos, conducción de calor de estado estacionario, dinámica de fluidos incompresibles, etc

Funciones armónicas- Potencial Complejo

Si para un caso particular encontramos una solución adecuada a la ecuación de Laplace sobre algún dominio D entonces podemos decir que la solución es una función armónica, es decir es una función de clase C² (continuas hasta las segundas derivadas con respecto a x e y) que satisface la ecuación de Laplace sobre el dominio D.

Las funciones armónicas están directamente relacionadas con las funciones analíticas de variable compleja, recordemos el teorema 26 de la guía de FVC:

Si una función es analítica en un dominio D, sus funciones componentes  y  son armónicas en D.

Además dichas funciones se llaman armónicas conjugadas, y dada una función armónica en un dominio es siempre posible encontrar su armónica conjugada para armar una función compleja que llamaremos Potencial Complejo:

.

Consideremos una curva paramétrica ,  con t real, que corresponde a una curva de nivel de  y derivemos con respecto a t:

El vector  es tangente a la curva en cada punto y es ortogonal al vector . De manera similar, las curvas de nivel de , son ortogonales al vector: . Si realizamos el producto escalar entre ambos vectores normales a las curvas y reemplazamos las ecuaciones de Cauchy-Riemann:  

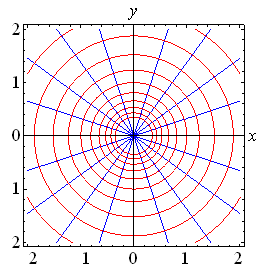
vemos que también son ortogonales. Por lo tanto las curvas    son ortogonales a las curvas . Como se observa en la figura para la función , en rojo las líneas para  y en azul para .

Un ejemplo simple de la aplicación del Potencial Complejo es determinar el potencial  y las líneas de campo eléctrico para alguna configuración de cargas eléctricas. El Potencial Complejo presenta dos ventajas:

·         resulta más fácil manipular una función compleja, que sus partes real e imaginaria por separado;

·         las curvas de se intersectan con las líneas equipotenciales formando un ángulo recto, lo que nos da la información directa de la dirección de las líneas de fuerza eléctrica.

Campo eléctrico

En el espacio que rodea a una o más cargas existe un campo eléctrico, y para cada punto de dicho espacio definiremos una intensidad del campo eléctrico, la cual señala lo que le ocurriría a una pequeña carga colocada en él. Pueden ser representados por líneas con flechas que, en el caso del campo eléctrico, señalan el sentido de la fuerza que actúa sobre cargas eléctricas positivas.

Potencial eléctrico o voltaje

El potencial eléctrico de un punto del espacio es, en relación a otro (definido como de potencial cero), igual a la razón entre la energía E que se requiere para transportar una carga de prueba y el valor de dicha carga. En una región del espacio libre de cargas, el potencial eléctrico verifica la ecuación de Laplace.

El conjunto de puntos que poseen igual potencial forman las que denominamos superficies equipotenciales. Las líneas de campo eléctrico son en todo punto perpendiculares a las superficies equipotenciales.

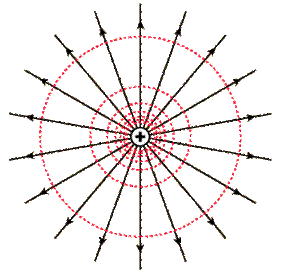
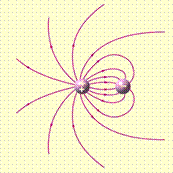
En la figura se ilustra una carga puntual positiva, líneas de campo en negro y superficies equipotenciales en rojo. Observe la analogía con el gráfico de

El concepto de líneas de campo fue introducido por Michael Faraday (1791-1867). Son líneas imaginarias que ayudan a visualizar cómo va variando la dirección del campo eléctrico

Propiedades:

·         El vector campo eléctrico es tangente a las líneas de campo en cada punto.

·         Las líneas de campo eléctrico son abiertas; salen siempre de las cargas positivas o del infinito y terminan en el infinito o en las cargas negativas.

·         El número de líneas que salen de una carga positiva o entran en una carga negativa es proporcional a dicha carga.

·         La densidad de líneas de campo en un punto es proporcional al valor del campo eléctrico en dicho punto.

·         Las líneas de campo no pueden cortarse. De lo contrario en el punto de corte existirían dos vectores campo eléctrico distintos.

·         A grandes distancias de un sistema de cargas, las líneas están igualmente espaciadas y son radiales, comportándose el sistema como una carga puntual.

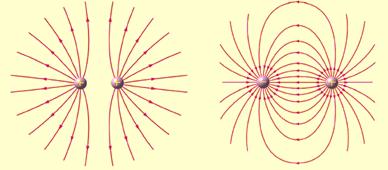
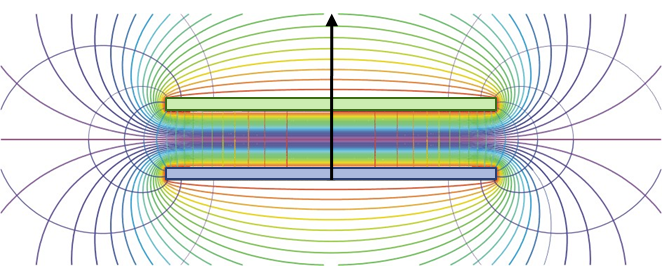
Representación de campos eléctricos creados por dos  cargas puntuales: de igual signo, signos opuestos y diferentes magnitudes:

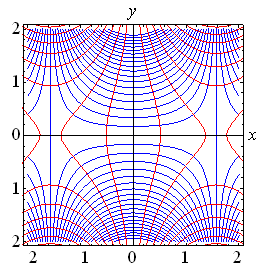
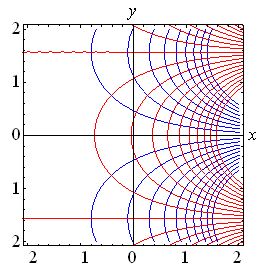
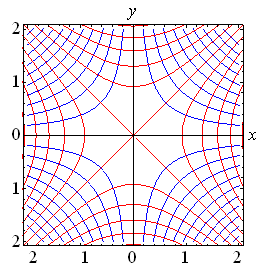
A continuación, gáficos para diferentes funciones de variable compleja donde se observa en rojo las líneas para  y en azul para :

Enlaces a Notas de Aplicación relacionadas:

Mauricio W. Arce, Análisis complejo aplicado a la Teoría del Potencial Eléctrico

Javier Alfonso Pesce, Aplicaciones de Propiedades de Funciones Armónicas y Transformaciones Conformes

Matias S. De Pilato, Aplicación Funciones Armónicas: Corriente en un transistor de efecto campo

Elio Rodrigo Cardozo, Aplicación de Transformaciones Conformes: Temperaturas Estacionarias

Leandro Sebastián Sánchez, Corriente en un transistor de efecto de campo

Cualquier consulta o sugerencia dirigirla a esta dirección.
Última modificación: 09-08-2019