A veces ser un genio no es algo sencillo… y más bien acaba complicándole a uno la vida….
Évariste Galois, el matemático que vivió rápido y murió joven
Sin lugar dudas resolver ecuaciones ha sido y es fundamental para todas las ciencias o tecnologías. Todos nos hemos enfrentado a las ecuaciones de primer grado y, posteriormente, a las de segundo grado. Y sabemos que las soluciones de la ecuación de segundo grado se expresan con la fórmula de Bháskara:
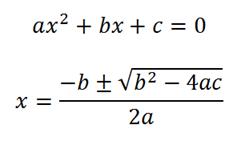
¿Y si en vez de una ecuación de segundo grado tratamos de resolver una ecuación de tercer, de cuarto grado? Pues desde el siglo XVI se conocen soluciones a este tipo de ecuaciones (naturalmente necesitan, en su expresión raíces cúbicas o cuartas).
Si bien se sabía cómo resolver las ecuaciones hasta grado cuarto desde el siglo XVI, pero las de grado cinco o superior se resistían. Hasta 1824, en este año, Niels Henrik Abel demostró que existen ecuaciones de grado mayor o igual a cinco que no se podían resolver mediante una fórmula que envolviera a los coeficientes de la ecuación ligados por operaciones algebraicas como suma, producto, división o raíces (de cualquier grado), lo que técnicamente se conoce resolver una ecuación por radicales. Sin embargo, otras ecuaciones sí que podían ser resueltas por ese método. Aquí es donde aparece la teoría de Galois que consigue, entre otras cosas, determinar exactamente qué ecuaciones pueden ser resueltas por radicales.
|
|
La leyenda de Évariste Galois lo describe como un genio precoz de las matemáticas, víctima durante toda su vida de la negligencia, la incomprensión y la mala suerte. Esta leyenda presta especial atención a la noche del 29 de mayo del 1832. Évariste estaba convencido que esa sería su última noche, a la mañana siguiente tenía un duelo y daba por segura su muerte. No tenía tiempo que perder y pasó la noche escribiendo el que sería su “testamento” matemático. Pese a su edad, sólo tenía 20 años, nadie duda que fue un gran matemático. Se puede decir, que su teoría es la que ha hecho posible el desarrollo del álgebra en los últimos 200 años, aunque no fue aceptada en vida cuando la presentó (los matemáticos de la época no la entendieron). |
Galois nació en Bourg la Reine, cerca de Paris en 1811. Aunque su legado matemático a tan pronta edad es innegable, no se puede decir que Évariste fue exactamente un niño prodigio, ya que sus primeros contactos con las matemáticas fueron a los 12 años, cuando comenzó a estudiar en Paris.
A los 15 años, y tras repetir curso (hasta algunos genios han repetido curso alguna vez), Évariste encontró en las matemáticas el reto intelectual que le faltaba, especialmente en el estudio del Álgebra, rama matemática que por aquel entonces tenía múltiples resultados sin resolver.
Tras ser rechazada en dos ocasiones su solicitud de acceso a la Escuela Politécnica de Paris, sí fue admitido finalmente en la École Normale. Allí su vida cambió, y su carácter polémico ayudó a que se convirtiera en un revolucionario político, teniendo muchísimos problemas e incluso estando una temporada en la cárcel.
Sobre el duelo que desembocó en su muerte hay varias versiones, la más extendida es que fue a pistolas, como una especie de ruleta rusa; estando cargada solamente una de las pistolas. Aunque al parecer fue a espadas, y su rival por desgracia para él, era el campeón de esgrima del ejército francés. Murió a causa de las heridas de la pelea, que le provocaron una peritonitis letal.
Los detalles que condujeron a su duelo no están claros, supuestamente a causa de un lío de faldas, una “infame coqueta”, como el mismo matemático apodó a la causante de su desgracia. Algunos sostienen que el duelo fue preparado por la policía y las facciones monárquicas para eliminar a un enemigo político, tal vez utilizando como cebo a una mujer.
Galois trabajó durante mucho tiempo en la obtención de una fórmula general válida para ecuaciones de grado 5 y superiores. Normalmente sus esfuerzos concluían en ecuaciones erróneas y más complicadas de resolver que la ecuación original. Finalmente demostró, casi simultáneamente con Niels Henrik Abel, la imposibilidad de encontrar una solución general a estas ecuaciones utilizando únicamente la suma, la resta, la multiplicación, la división, la exponenciación y la radicación de los coeficientes (es decir, mediante radicales). Llegó a la conclusión de que dichas ecuaciones solo pueden resolverse de forma aproximada utilizando técnicas de cálculo numérico. Sin embargo, existen muchas ecuaciones de grado 5 y superiores perfectamente resolubles mediante radicales. Son casos particulares, pero Galois enunció y demostró un teorema (Teoría de Galois), para identificar dichas ecuaciones.
Su trabajo sobre teoría de ecuaciones fue presentado varias veces, pero no llegó a ser publicado en vida. El primer intento de publicación fue rechazado por Cauchy en 1829, el mito de Galois acusa a Cauchy, católico y monárquico, de ser el responsable de “uno de los más grandes desastres de la historia de las matemáticas”, al “perder” u olvidar los escritos de Galois. Aunque los motivos para el rechazo siguen siendo poco claros, pues tenía puntos en común con un reciente artículo publicado por Abel, parece ser que Cauchy sí reconoció la importancia del trabajo de Galois y que simplemente le sugirió algunos cambios. Además se han encontrado cartas de Cauchy en las que hablaba de Galois y de su intención de presentar ante la academia su trabajo.
|
|
|
Galois, tras seguir el consejo de Cauchy, lo volvió a intentar otra vez en febrero del 1830 enviándolo esta vez al secretario de la Academia, en aquel tiempo Fourier, para que lo considerara para el Gran Premio de Matemáticas. Aquí la fortuna volvió a jugar otra mala pasada al joven Évariste, Fourier murió poco después y la memoria se perdió. Sin embargo, la leyenda de Galois esta vez culpa a Fourier de ser incapaz de comprender el escrito de Galois y “perderlo” intencionadamente, tal como lo había hecho antes Cauchy, y acusó a la academia de una farsa para desacreditarle. El premio fue a parar a Abel, quien había muerto de tuberculosis recientemente (1829).
La más importante de las contribuciones de Galois fue una nueva demostración que no existe una fórmula quíntica, es decir que una ecuación de quinto grado o superior no puede ser siempre resuelta mediante radicales, además del desarrollo de técnicas que permitían determinar cuales de estas ecuaciones sí que lo eran. Aunque Abel ya lo había demostrado en 1824, los métodos de Galois pusieron las bases para lo que hoy es llamado Teoría de Galois.
En 1843, once años después de su muerte, Joseph Liouville publicó esta teoría defendiendo la autoría de Galois. Revisó sus manuscritos y declaró que aquel joven en verdad había resuelto el problema de Abel por otros medios que suponían una verdadera revolución en la teoría de las matemáticas empleadas. El manuscrito fue publicado en el número de octubre de 1846 del Journal des mathématiques pures et appliquées.
Videos:


