Con integrales que dependen de algún parámetro, es decir integrales paramétricas, se pueden definir funciones de manera similar a cuando usamos series de funciones (ver conv. Unif)). Estas funciones tienen como dominio de definición a la región de convergencia.
Ejemplos de Integrales Impropias Paramétricas y Convergencia Uniforme:
Al integrar una función, continua o continua a tramos siempre se suaviza y resulta continua. Pero esto no pasa siempre con las integrales Impropias que dependen de parámetros, como se ve en los siguientes ejemplos:
i) Observe la discontinuidad de la siguiente función definida por medio de una integral impropia:
 |
 |
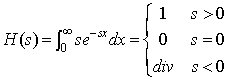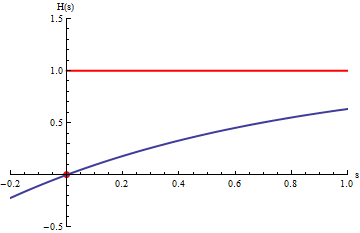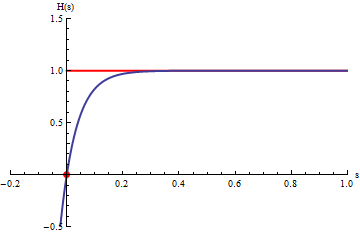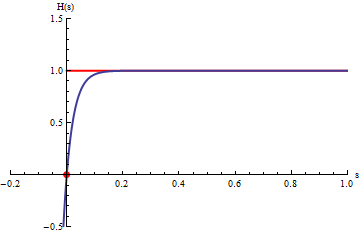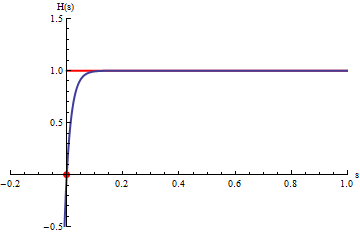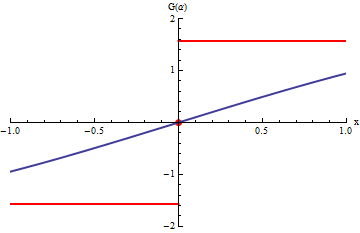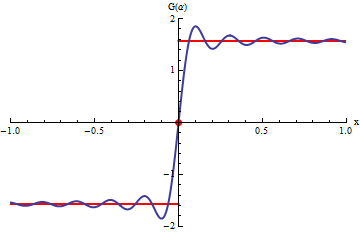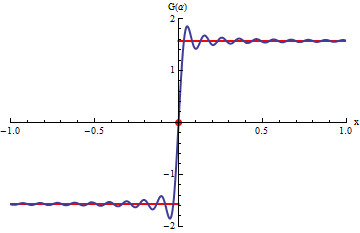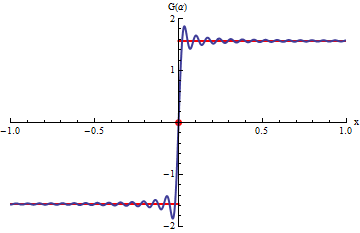
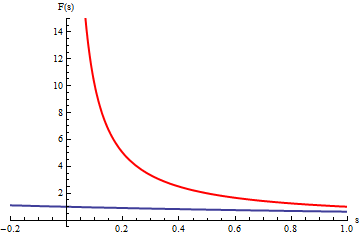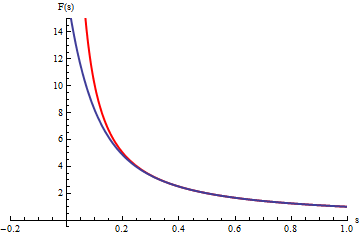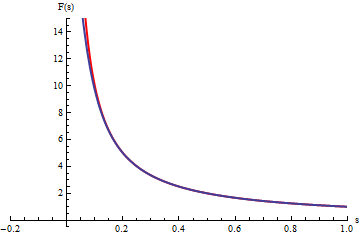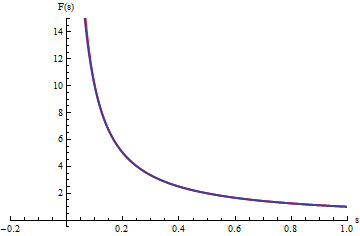
En el gráfico, las curvas en azul corresponden a las integrales
.
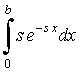La animación corresponde a variar b.
Cuando b tiende a
infinito las curvas azules se acercan a la curva roja que corresponde a la
integral impropia:
.
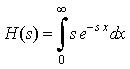Otro ejemplo lo muestra la siguiente integral impropia que también converge a una función discontinua:
 |
 |
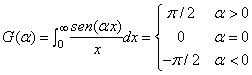ii)
¿se pueden intercambiar integrales y
derivadas? Si volvemos al ejemplo de la función G, se puede afirmar que: ¿
?
Si bien G tiene derivada nula en todo
punto excepto el origen donde no es derivable, cambiando el orden, primero
derivamos y luego integramos, es decir nos queda la integral
, esta última diverge para casi todo
.
iii)
En cambio para
.
 |
 |
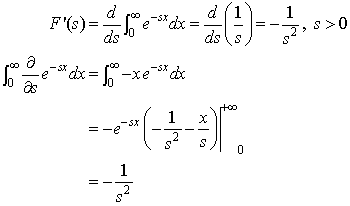coincide si derivamos la función F o si primero derivamos y luego integramos. En este caso vale intercambiar integrales y derivadas. Esto está directamente relacionado con la convergencia uniforme.
Ver en la guía los Teoremas 14 15 y 16, sobre continuidad, integración y derivación de funciones definidas por medio de integrales impropias.
.