Interpretación gráfica de la Convergencia Uniforme de Series de Funciones:
Dada una serie de funciones (los términos son una sucesión de funciones de x)
decimos que
converge uniformemente en un conjunto
P, según la definición 20 de la guía, si para todo
positivo encontramos un N
(
) tal que:
.
Si
consideramos que el conjunto P es el intervalo [a,b], la
interpretación gráfica de la definición de convergencia uniforme consiste en que
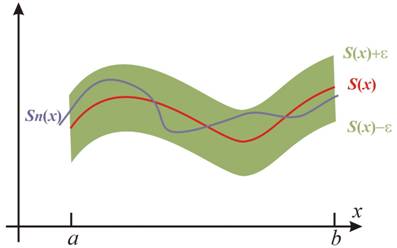
la curva de la función suma parcial, Sn(x), queda dentro de un
tubo centrado en la curva de la función suma, S(x), de ancho 2
,
y esto vale para todo n mayor que N. Es decir, es necesario sumar
una cantidad mínima de términos (N), que depende del ancho del tubo y es
el mismo para todos los x en el intervalo. Como se ve en el gráfico:
En la convergencia puntual, se fija un punto x1 en el intervalo, se reemplaza en la serie de funciones resultando una serie numérica que suponemos convergente, es decir dado un ancho del tubo se encuentra un valor de N para ese punto. Pero si cambiamos el punto por otro x2 en el intervalo, la serie numérica resultante es diferente y por lo tanto el valor N no tiene por qué ser el mismo. Justamente esta es la diferencia con la convergencia uniforme, pues cuando es uniforme, el valor de N es el mismo para todos los puntos del intervalo.
En la práctica el estudio de la convergencia puntual se reduce a calcular para cada x fijo, el límite de Sn(x), cuando n tiende a infinito. Mientras que para la convergencia uniforme se utiliza el test de Weierstrass (pues para realizarlo por límite habría que estudiar por definición la dependencia o no de N con x).
Observación: La convergencia uniforme siempre se refiere a un conjunto. No tiene sentido decir que una serie converge uniformemente si no se aclara inmediatamente en qué conjunto se da la convergencia uniforme. Siempre un conjunto donde la serie converge uniformemente será un subconjunto de la región de convergencia puntual de dicha serie.
-
Por ejemplo, la serie de funciones del ejercicio 7 (a) del Práctico 1,
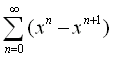
cuyas sumas parciales son:
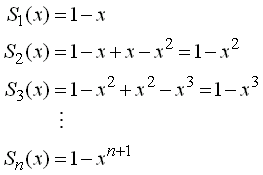
y converge
puntualmente en el intervalo (-1,1]. Consideramos dos subconjuntos interiores a
ese intervalo y formemos un par de tubos correspondientes con
= 0.1
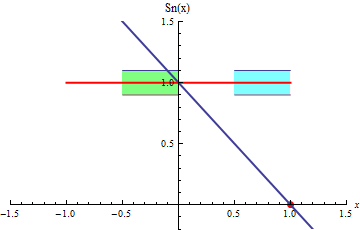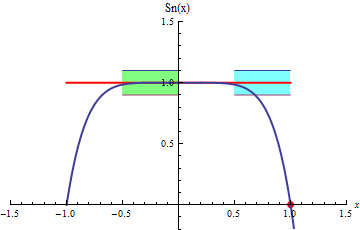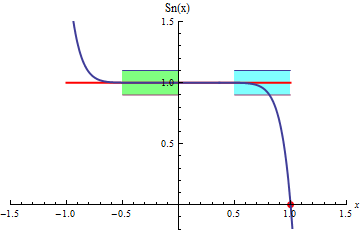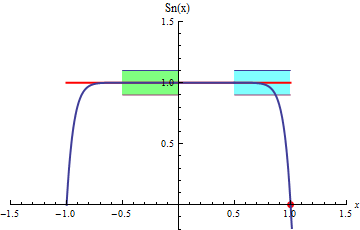
al rededor de la función suma. En la siguiente animación se ve en
curvas azules como las sumas
parciales convergen rápidamente a la función suma
(en rojo) y quedan contenidas dentro del tubo en el
intervalo [-0.5,0], sin embargo esto no sucede en el intervalo [0.5, 1]. En el
primer intervalo la convergencia es uniforme y en el segundo no lo es.
Obsérvese que la función suma es discontinua en (-1,1]. Por lo tanto, según el teorema 12, la convergencia de esta serie de funciones no puede ser uniforme en todo el intervalo (-1,1].
- Una animación similar podemos ver para la serie
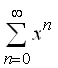
que
converge puntualmente en el intervalo abierto (-1,1) a la función
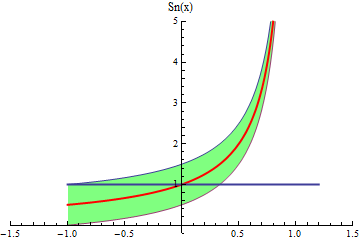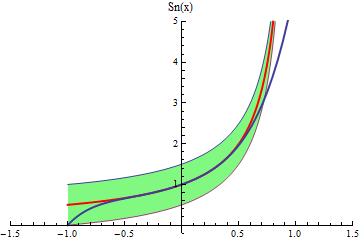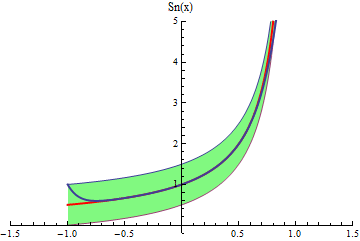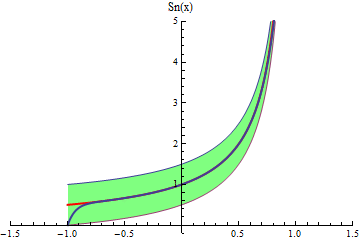
Si bien la convergencia uniforme no se da en toda la región de convergencia, veamos por el test de Weierstrass que converge uniformemente en el intervalo [-1/2,1/2].
Como los valores de x en el intervalo verifican
podemos acotar el termino general
por términos mayorantes que corresponden a la serie geométrica
que es convergente.
Luego por el test de W. podemos asegurar la convergencia uniforme
de la serie 
en intervalo [-1/2,1/2].
En realidad se podría tomar un intervalo mayor: [-a,a] con 0<a<1 , y probar la convergencia uniforme procediendo de manera similar. En cambio no se pode probar la convergencia uniforme en el intervalo abierto (-1,1).