Funciones de Variable Compleja (FVC)

Ondas y Espectros

Vivimos rodeados de ondas,  pero.. ¿qué es una onda?

ü  Una perturbación que se propaga en el espacio y en el tiempo a través de un medio, transmite energía pero no materia.

ü  Las ondas más interesantes de la naturaleza son periódicas. Eso quiere decir que no es una única perturbación la que viaja, sino que son muchas (muchísimas) perturbaciones, una atrás de la otra, todas iguales y equiespaciadas. Eso es una onda periódica.

Mecánicas: se propagan en medios materiales: ondas elásticas, sonido, en el agua (al arrojar una piedra), mareas, sísmicas

Electromagnéticas: se propagan por el espacio sin necesidad de un medio: televisión, radio, AM ,FM, WiFi, microondas, rayos X, luz, infrarrojos, ultravioleta, etc

¿Cómo representarlas en forma matemática?

Las más simples son las ondas armónicas, usando funciones trigonométricas (o exponenciales complejas)

Características de las ondas:

l:	Longitud de onda distancia entre dos picos consecutivos		[m]
A:	Amplitud  máximo desplazamiento de una partícula
T:	Periodo  tiempo entre dos crestas		[seg]
f:	Frecuencia número de oscilaciones por unidad de tiempo en un mismo punto		[Hz]
k:	Número de onda angular		[rad/m]
w:	Frecuencia angular		[rad/seg]

Cuando la onda periódica no es simple, siempre la podemos pensar en su desarrollo de Fourier, donde además de la frecuencia fundamental aparecen sus múltiplos o “armónicos”. Vemos estas características en el siguiente ejemplo.

Sonido u ondas sonoras:

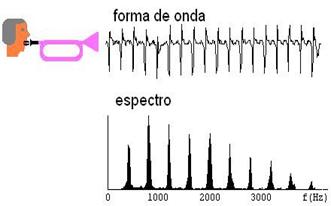	En el sonido la altura, tono, grave-agudo, se refiere a la frecuencia [Hz]. El nivel de Intensidad a la Amplitud [dB] y el Timbre (claro, brillante, apagado) a su espectro en frecuencia, y la envolvente (ataque-sostenimiento-desvanecimiento). Cuando los instrumentos musicales, piano, guitarra, flauta, emiten la misma nota, por ejemplo el La central (440Hz) ¿por qué los diferenciamos? Si están bien afinados, sus ondas tienen la misma frecuencia fundamental, sin embargo difieren en el Timbre, en sus armónicos. Es decir sus espectros en frecuencia tienen patrones diferentes. Recordar los gráficos de espectros vistos en funciones sencillas. Cuando se usan Ecualizadores, se están afectando directamente los coeficientes de Fourier correspondientes a pequeñas bandas de frecuencias.
Es decir, el oído puede distinguir dos notas con el mismo tono y la misma intensidad que provengan de instrumentos diferentes. Los sonidos producidos por estos instrumentos, no serán exactamente iguales, tienen timbres diferentes pues sus espectros en frecuencia tienen patrones diferentes. Con la teoría de las series de Fourier entendemos que una nota (sonido emitido por un instrumento) es la suma de muchas ondas sonoras de frecuencias diferentes. Una nota no es, entonces, un sonido puro. La onda de frecuencia más baja se llama sonido fundamental o primer armónico. Las otras, son una serie de ondas secundarias, con frecuencia múltiple de la primera. A todas estas ondas las llamamos armónicos.
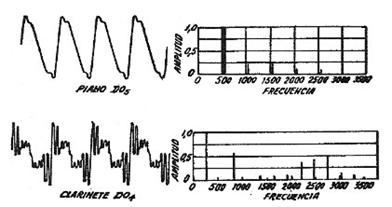Dependiendo del instrumento que emita la onda sonora, los armónicos serán diferentes. Este hecho es el que produce que el Do de un piano no suene igual al Do de un clarinete. Esta calidad sonora recibe el nombre de timbre y está directamente relacionado con los espectros en frecuencia.

La onda producida por una cuerda vibrante.

La nota producida por una cuerda vendrá determinada por la longitud (L), la tensión (T), la densidad (d) y la sección (S). Así, si disponemos de una cuerda muy tensa y fina, obtendremos una nota aguda; y por el contrario, si la cuerda está poco tensa y es gruesa, la nota será grave.

De hecho, la frecuencia se puede encontrar a partir de la fórmula:

Veamos ahora la relación gráfica entre la longitud de una cuerda (L), la frecuencia (f) y longitud de oscilación de una onda (l) producida al hacer vibrar la cuerda.

Vamos a ver también cuáles son los diferentes sonidos (armónicos), que obtendremos al hacer vibrar la cuerda. Para eso debemos de tener en cuenta que siempre tiene que haber un nodo en los extremos de la cuerda. 

Si repitiésemos este proceso indefinidamente, obtendríamos todos los armónicos del sonido. Su frecuencia se obtiene multiplicando la frecuencia fundamental por todos los números naturales.

Estas relaciones entre las frecuencias dieron pié a los pitagóricos a construir una escala musical que se basaba en la relación armoniosa entre las notas.

Dividiendo las frecuencias de un armónico con el anterior se obtienen los intervalos que se utilizan para construir la escala musical.

•  2f1/ 1f1 = 2/1 (la octava)
•  3f1 /2f1 =3/2 (la quinta)
•  4f1/3f1 =4/3 (la cuarta)
•  y  así sucesivamente...

Todos estos sonidos son los que denominan la escala de los armónicos. 

Cualquier consulta o sugerencia dirigirla a esta dirección.
Última modificación: 03-10-2019