Ejemplo de cómo encontrar un desarrollo en Serie de Laurent:

Analicemos los posibles desarrollos en series de Laurent de la función

 ,

Si elegimos el punto z0=2 como centro de los desarrollos,  vemos que podemos trazar dos radios desde el centro hasta los puntos singulares de la función, (z=i y z=-1 ).

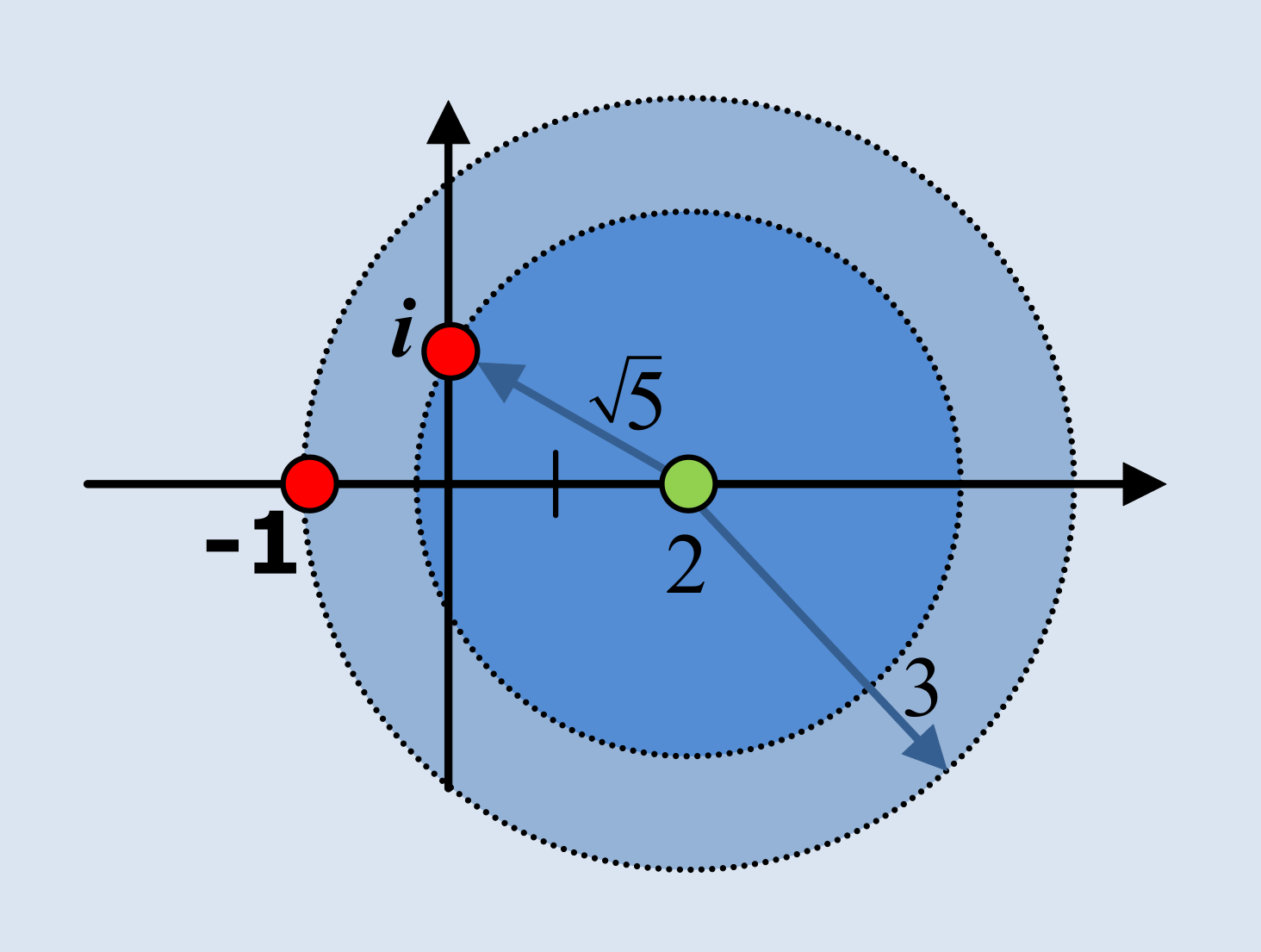
Esto define tres posibles regiones:

Por lo tanto hay tres desarrollos de Laurent centrados en el punto z=2 para la función dada.

Veremos cómo encontrar el desarrollo para el anillo

Para comenzar separamos en fracciones simples:

En cada término vamos a utilizar el desarrollo conocido de la serie geométrica

Debemos primeramente acomodar para que el desarrollo quede centrado en z0=2 , es decir que las series resulten en potencias de (z-2).

A continuación encontramos un desarrollo para el primer término, desplazamos el centro sumando y restando z0, luego sacamos factor común adecuadamente y utilizamos el desarrollo de la serie geométrica:

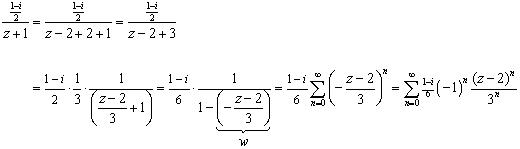
Es decir, en este caso consideramos como la razón geométrica a

Por lo tanto la serie para el primer término converge cuando

 es decir:

Con el segundo término procedemos en forma similar, en este caso sólo cambiamos el factor común, z-z0, para que esta expresión quede en el denominador de la razón geométrica, así la región de convergencia es el exterior de un círculo:

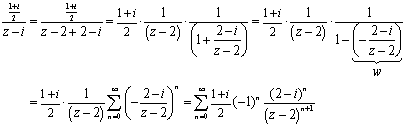
Este último desarrollo converge cuando

 es decir:

Sumando ambos términos, la región de convergencia es al menos la intersección:

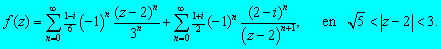
 Procediendo en forma similar, luego de acomodar el primer término (sumamos y restamos 2), tenemos dos opciones, sacar factor común en el denominador el número 3 ó sacar factor común (z-2):

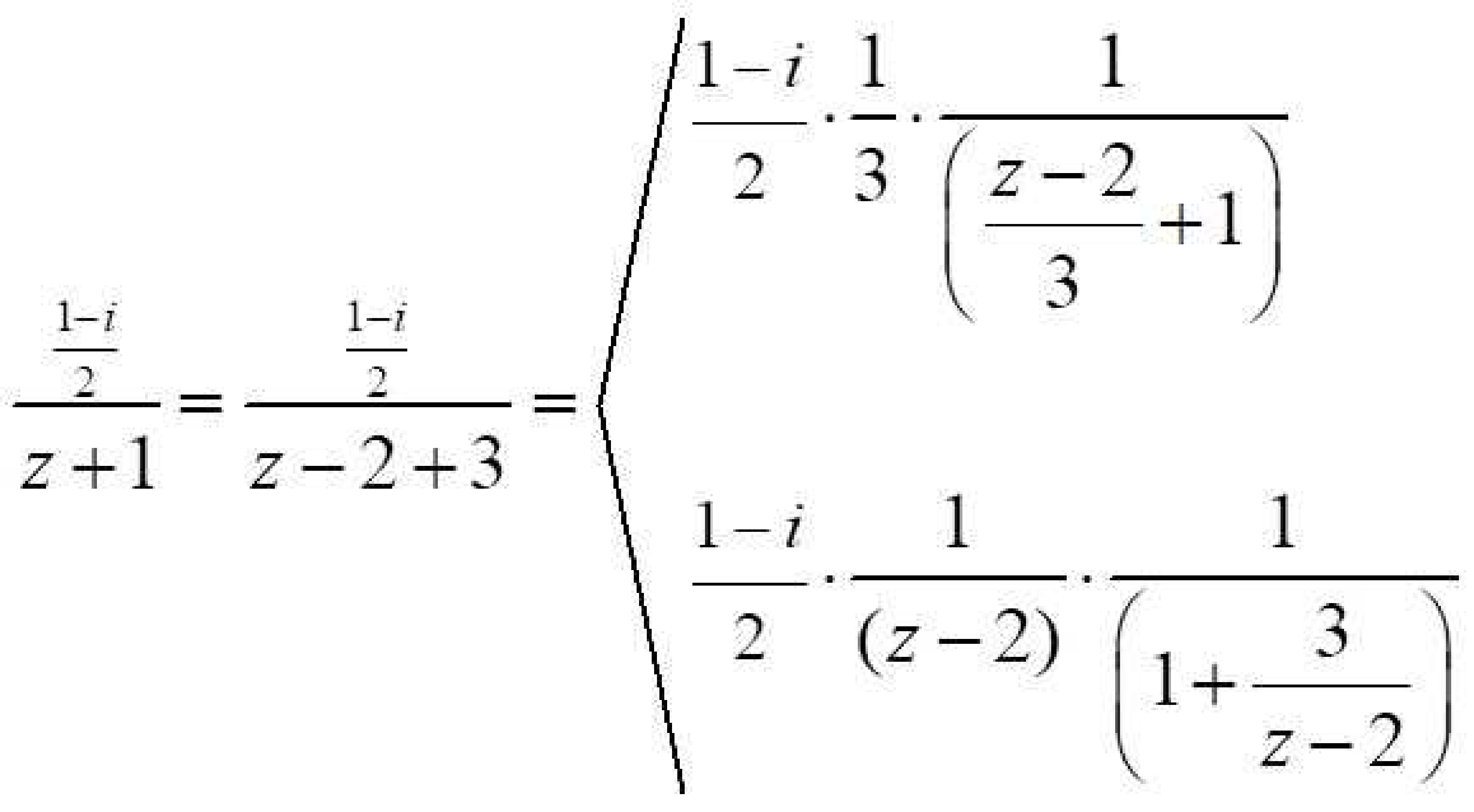
Esto conduce a dos posibles desarrollos para el primer término de la función. Uno en el interior de un círculo de radio 3 y el otro en el exterior.

En el segundo término sucede algo similar, podemos sacar factor común en el denominador (2-i) ó (z-2):

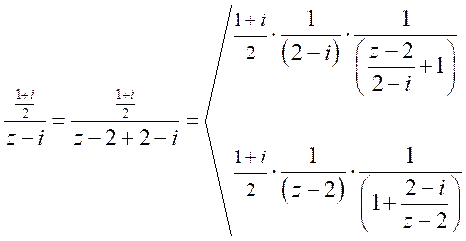
Usando el desarrollo de la serie geométrica podemos obtener dos desarrollos para este término uno dentro  de un círculo y el otro en el exterior (eligiendo convenientemente cuál es la razón geométrica w).

Por lo tanto tendríamos dos desarrollos para cada término de la función. Si combinamos  estos 4 desarrollos obtenidos, sumando adecuadamente uno por cada término, obtendremos los tres desarrollos de Laurent de la función dada (hay una combinación que no tiene sentido pues  la intersección de las regiones es vacía).

¿Te animás a encontrar los otros dos desarrollos?